こんにちは!真友ジャンプ!です!
小学校4,5年生になると、「分数」をフル活用する機会が増えてきます!
特に、5年生になると、「通分」や「約分」等やっかいなポイントが増えてきます!
そして、さらに大変なのが、この「通分」や「約分」の要素を使うため、邪険には扱えないということです!
この記事では、そんな「通分」のポイントや「通分」をスムーズに行うためにやってポイントを確認していきたいと思います!
そもそも通分って?
まず、通分とは、「2つ以上の分数の分母をそろえる」ということです!
これは、足し算や引き算の計算を行う時に使います!
足し算や引き算を行う上で、分母を揃えなければ、比べられないからです!
例えば、次のような計算で…
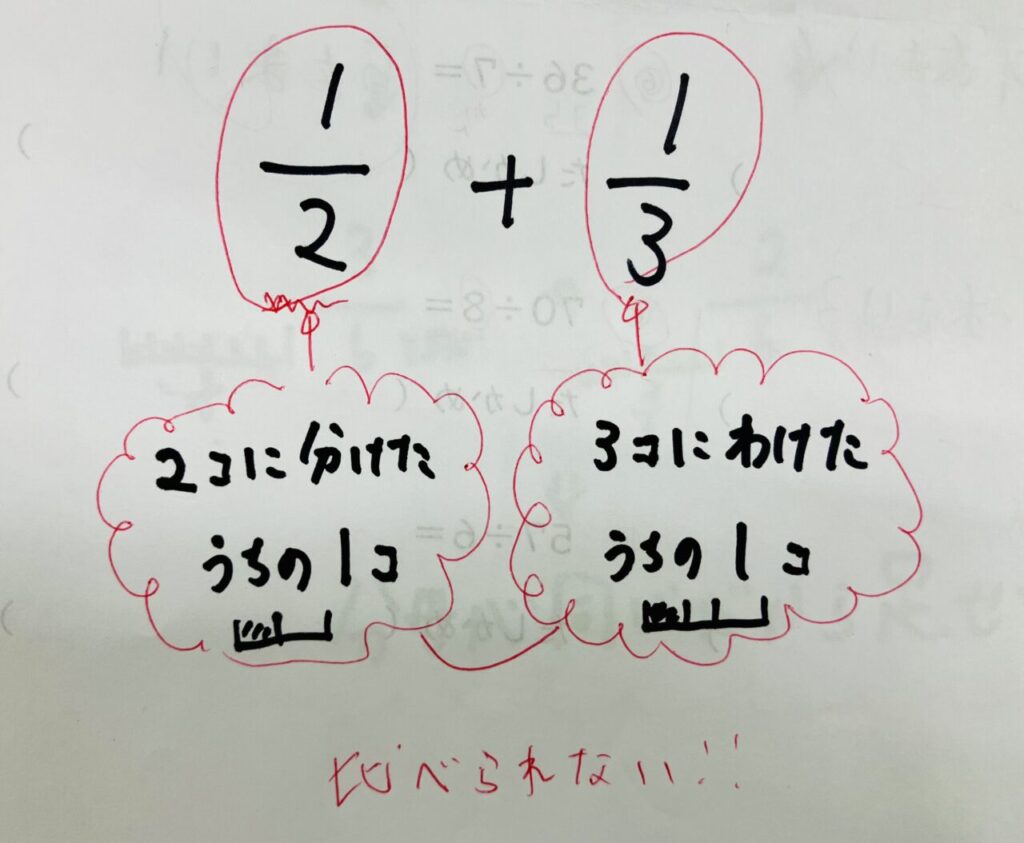
2分の1⇒2個に分けたうちの1つ
3分の1⇒3個に分けたうちの1つ
となるので、これを足す(引く)となった時に、計算では数字を出せなくなってしまいます。
そこで、「何個分の何個」の「何個分」(分母)の方を揃えることができると、分子の方で、たす、ひくの計算を行うことができるようになります!
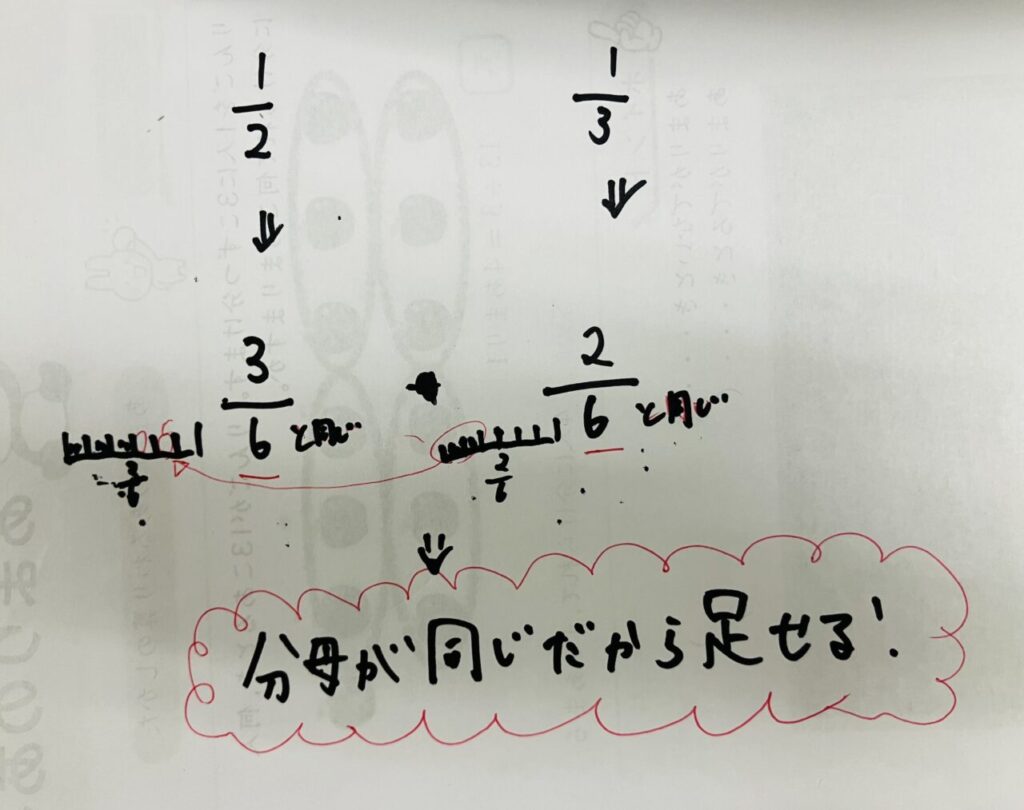
この分母を揃える時に、「分母に掛けた数を分子にも掛ける」のが、通分となります。
通分につまづきを感じた際に、確認しておきたいポイント
では、「通分」でつまづいたと感じた際に、確認しておきたいポイントを紹介したいと思います!
九九が頭に入っているか
通分は、分母や分子に数を掛けて行うため、かけ算は必須となってきます。
そのため、九九の計算がパッとできるようになっておくと、通分の上での計算もスムーズに行えるようになります!
また、「どの段に何の数があるか?」を考えていくことも大切になります!
最小公倍数の考え方が理解できているか
分母を揃えるということは、同じ数になるようにかけ算を行うということです。
そのためには、九九もそうですが、同じ5年生で習得する、「最小公倍数」や「公倍数」の考え方も理解しておく必要があります。
そして、前述した九九とも繋がる部分ですが、「どの段にどの数があるか」を理解しておくとスムーズです!
2桁×1桁のかけ算、2分の1や3分の1、2桁÷1桁のわり算ができるか
九九の計算以外の、「2でかける」「2で割る」の計算は、九九に隠れて見落とされがちですが、ここがスムーズに行えるかどうか?という部分も大きくかかわってきます。
特に「2桁÷1桁」のうち、「商が2桁になる計算」については、約分の計算でも多用する部分なので、できるかどうかを確認してみれるといいですね!
通分でつまづきを感じた時に、確認しておきたいポイントを軽く紹介させていただきました!
小学生に限らず、中学生でも大事な分野でもあるので、「この冬のうちに確認しておきたい」と感じましたら、御気軽にお問合せください!
冬の入会キャンペーン
冬のスペシャルコース!(冬期講習)
メールフォーム

この冬の講習をきっかけに子どもたちが自信をつけて笑顔になり、希望をもてるようにサポートします!
